\'{a} \`{a}

Voilà exactement comment comprendre le tableau présentant les groupes anneaux et corps

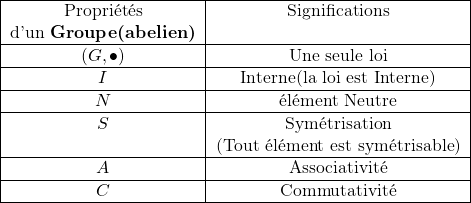
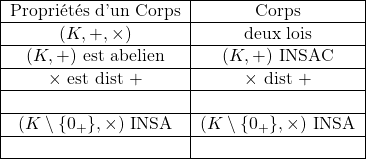
Pour la stabilité par combinaison linéaire: 

rappelons la définition:

N.B: faire attention à la finitude de la somme.

En effet cela signifie que toute somme finie d’élément de est encore un élément de . de plus si en faisant la somme finie on fait agir des scalaires quelconques sur les termes de la somme, on obtient toujours un élément de . La stabilité signifie qu’on ne sort pas de l’ensemble dans le quel on prend les éléments.

Exemple de calcul du rang d’une Famille de vecteurs:

Ce qu’il faut comprendre:

1. En appliquant la définition du rang d’une famille de vecteurs il faut trouver la dimension de l’espace vectoriel engendré par les vecteurs donnés. c’est ce qui est noté:
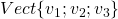
2. De plus l’écriture: 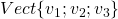 stipule que  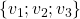est une famille génératrice de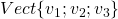
3. Il faut donc en extraire une base ou encore une famille libre maximale contenue dans la dite famille.
4. mais comme on n’a que trois vecteurs, cette famille ne peut avoir que 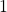,  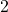 ou trois vecteurs. Mais comme les vecteurs sont liés, il ne reste plus que deux choix: soit 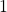soit
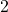
5. ainsi si deux vecteurs quelconques sont libres on a terminé! et le rang est 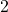. ce qui est le cas dans l’exemple!
6. mais pour arriver à 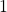il faudrait s’assurer que chaque fois qu’on prend deux vecteurs quelconques parmi les trois ils sont toujours liés!

La méthode d’écriture de l’un en fonction des autres permet de raffiner la preuve!

bonne suite!